Examples¶
Solution
You can solve this by considering the time dilation for an earth observer, as the lifetime is with respect to the rest frame! The lifetime for an earth observer is therefor stretched to s. Therefore muons only need to travel about 4 lifetimes, and a decent fraction () can still be measured on the earth surface. You can also reason via length contraction of the path the muons travel 20 km.
Exercises¶
Answers¶
Solution to Exercise 1
Denote Mission control by and the spaceship by . According to S, the distance to the planet is . Thus the traveling time will be , with the velocity of the spaceship according to . time dilation
Requirement:Length contraction:
According to the astronauts, the planet is approaching them with a velocity .
So they have to waitin S’ a light pulse every year. Define event = n pulse . The (n+1) pulse Transform to via inverse LT
The n arrives at earth after traveling the distance with the speed of light. Hence, the moment of receiving is:
Similarly for the (n+1):
So, we conclude that the time between receiving two consecutive pulses by Mission Control is:
Is that possible?
The astronauts send 30 reports while on their way to the planet as their journey to the planet takes 30 years. According to this journey takes . The last pulse is send 50 years after has left earth. This pulse need to travel 40ly and that takes 40 years. Thus it is received after 90 years. In those 90 years, 30 pulses have been received, hence Mission Control receives a pulse every 90/30 = 3 years.
This is a great example, that you need to be careful with quick answers based on time dilation. That would give in between two pulses. But than we have forgotten that these pulses are not send from the same location.
Solution to Exercise 2
Events:
E0 - pulses send:
E1R - forward traveling pulse hits front mirror:
E1L - backward traveling pulse hits back mirror:
E2 - pulses send:
LT the events to
E0:
E1R:
E1L:
E2:
right pulse: first part of the traveling time is longer as the right mirror moves away, but on the way back approaches the pulse. The left pulse does exactly the opposite: first going to a mirror that is approaching and then moving after that is ‘running away’.
This becomes evident in the diagram.
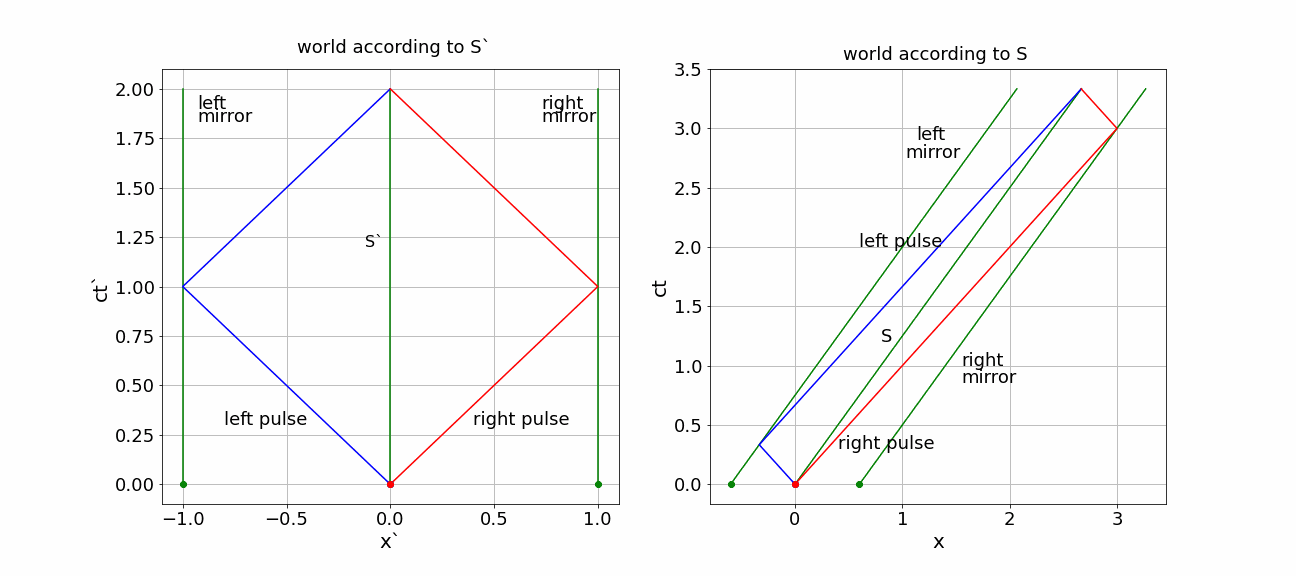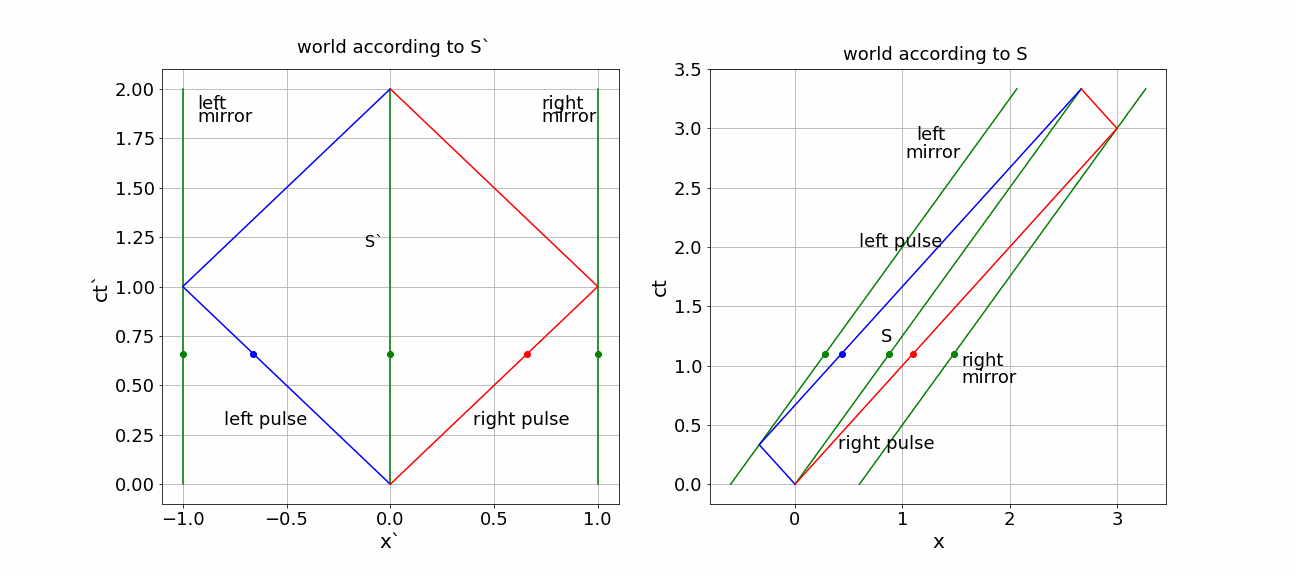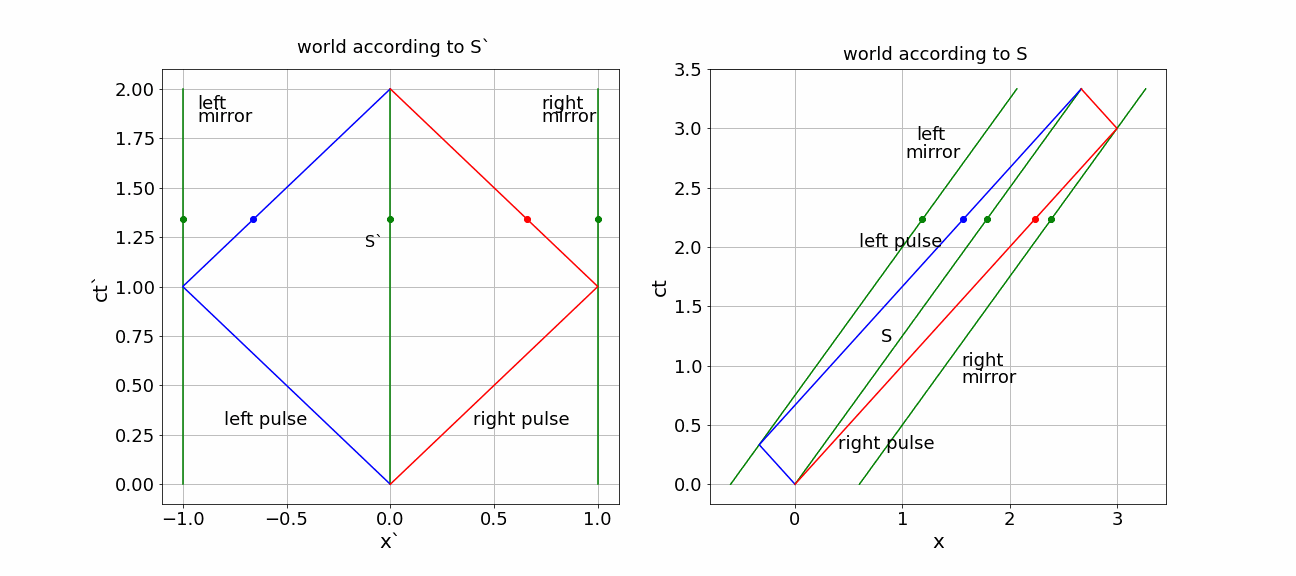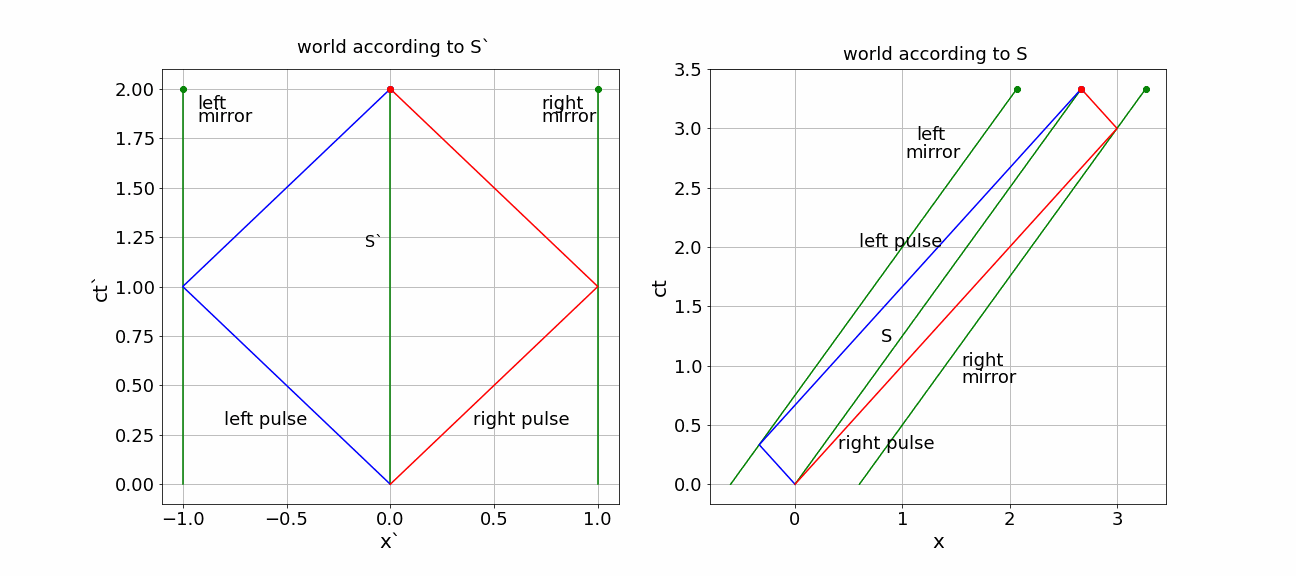
Figure 1:(x,ct) diagrams for S’ and S)
Solution to Exercise 3
E1:
trajectory object according to linear motion with velocity :
collision with
Thus, E2:
according to observer :
So, according to the object hasn’t moved! In retrospect, this is logical: sees moving at velocity and also sees the object moving at . Thus in the object has zero velocity.
Note: we will come back to the transformation of velocities. That is more subtle than it know may look.
Solution to Exercise 4
Special Relativity with LT
E1: en
LT naar with and :
velocity According to :
According to :
Thus the magnitude of the velocity according to is less than c.
Newtonian mechanics with GT
E1: en
GT:
GT naar with :
velocity According to : as before.
According to :
Thus the magnitude of the velocity according to is higher than c.
We will come back to this peculiar result in the world of Einstein and Lorentz.