As we discussed, in the second half of the nineteenth century it became clear that there was something wrong in classical mechanics. However, people would not easily give up the ideas of classical mechanics. We saw that the luminiferous aether was introduced as a cure and as a medium in which electromagnetic waves could travel and oscillate. Moreover, Lorentz and Fitzgerald managed to find a coordinate transformation that made the wave equation of Maxwell invariant. Fitzgerald came even up with length contraction: if the arm moving parallel to the aether of the interferometer of Michelson and Morley would contract according to then, the M&M experiment should result in no time difference for the two paths, in agreement with the experimental findings. However, there was no fundamental reasoning, no physics underpinning the transformation and the length contraction. It worked, but had an ad hoc character. Very unsatisfying for physicists!
And as we have mentioned, it took the work of a single man to change this and underpin the Lorentz Transformation, making Classical Mechanics a valid limit of Relativity Theory, only applicable at velocities small compared to the speed of light and to small distances compared to those of interest in cosmology.

Figure 1:Albert Einstein (1879-1955). Picture from Wikimedia Commons, public domain.
Lorentz Transformation
with
But there is more! Einstein also changed our view on the universe and on time itself. In the world of Newton and Galilei, people could not even think about relativity of time. Of course time was the same for everyone. There was only one time, one master clock - the same for all of us. It is hard coded in the Galilean Transformation:
Galilean Transformation
Now, if we compare GT to LT, we see that with the Lorentz Transformation this is no longer true: different observers may have different time. We will see that this has very peculiar consequences, some of which are very counterintuitive. However, they have been tested over and over again. And so far: they firmly hold. And there is no other way than to accept that the world and our universe is different from what we thought and from what we experience in our daily lives.
Do note, that the Galilei Transform is a limit of the Lorenz Transformation. If we let , we see that and . And this gives us: and , that is the Galilean Transformation! Now, this should not come as a surprise (even if it for a moment did). After all, Classical Mechanics does an outstanding job in many, many physics problems and the agreement with experiments is excellent.
The Lorentz Transformation¶
The way we wrote down the Lorentz transformation is a bit particular in a sense that we combine time with the speed of light into the “time” axis which now has unit length. We can do this as is constant for all observers independent of their frame of reference. The speed of light is said to be a Lorentz invariant. In this notation the transform between and (moving with velocity away) is easy to remember!
S and S’¶
We will discuss most of the consequences for two observers and , traveling with a constant velocity with respect to each other. They have taken their , resp. axis parallel to . Hence, we only need to talk about , knowing that this is the only component of the relative velocity between the two observers and that it is along the axis.
Furthermore, their and coordinates are taken in the same direction. This also holds for the -component. Finally, when and pass each other (they are then both at the same point), they put their clocks to zero: and .
Note: is sitting in her origin (with coordinates, according to ) and stays there. Similarly for who is sitting in (with coordinates, according to ).
The standard sketch is given in the figure below.
Figure 2: and : relative velocity parallel to the and axes.
N.B. It is crucial to be very precise in your notation when it comes to coordinates and quantities. For instance: might talk about the -component of the velocity of an object and denote this by . , on the other hand can also talk about that component, but will not call it the -component: in the world of “does not exist”, only does. So it is better to write for the -component of the velocity of the object according to . It may look cumbersome, and to a certain extent it is, but it actually does make sense. would say that this component is both space and time having a prime. Hence, naturally would talk about or
Lorentz Transformation and its inverse¶
The Lorentz Transformation, like the Galilean Transformation is a communication protocol for and . It allows them to interpret information that they get from each other in their own ‘world’, i.e. coordinate system.
For instance, if sees an object moving with , can ‘translate’ this information via the Lorentz Transformation into and or so if applicable. Of course, also needs such a translation scheme when receiving information from . That is: needs the inverse transformation.
Luckily, the inverse is very easy to reconstruct from the Lorentz Transformation itself. LT from to is
The inverse is found by invoking ‘relativity’, after all it is called Relativity Theory. If sees moving at a constant velocity , then - because motion is relative- will say that moves with . And thus, if writes down the Lorentz Transformation, she uses .
The inverse is therefore given by
with the Lorentz factor . Note that as is quadratic in , both and use the same value! That is why we don’t talk about : it is equal to .
The structure of the formulas is very symmetric and therefore needs little remembering.
From the Lorentz transformation it is clear that time is not universal anymore ( in general). This is a large step from Newton and Galileo. Now the time coordinate is mixed somehow with the space coordinate depending on the speed .
Lorentz factor¶
The Lorentz factor (or -factor)
is a dimensionless constant depending on the ratio of the velocity to the speed of light . Sometimes this ratio is abbreviated further as . For the ratio we know that it is smaller than 1 as is a limit velocity. From that it follows that the -factor is always equal to or larger than one, .
In many exercises the speed is given already as fraction of , e.g. . Analytically only for very few speeds a nice -factor is computed. These are for instance
Note that this list goes on for ever: there is a simple rule to find the triplets. Think about it yourself. Hint: the first one uses , the third one . What is special about them?
and .
Do you see the pattern? Can you derive the general rule? What is the next one? How about ?
In the limit¶
In the limit of low speeds with respect to the speed of light . Practically, this happens for about . In this limit the Lorentz transformation also reduces to the Galilean Transformation.
In the limit of infinity speed of light () the -factor is again one: and the ratio . Also here the LT reduces to the GT. The case of infinite speed of light represents the case that GT is generally valid, i.e. .
It is always important to verify that an extension of a well-established theory reproduces the results of that theory in the domain where it has been experimentally validated.
Length contraction & Time dilation¶
First Implications¶
As we have seen, we need to use the Lorentz Transformation instead of the Galilei one when two observers, and , want to exchange information. What changes if we do so? Let’s first do some examples and see some of the consequences and the ‘strange’ conclusions we need to draw.
Note: we will frequently use high velocities and large distances. It is convenient not to write these in units like and . The numbers in front of them become so large that keeping an overview becomes cumbersome. Therefore, we will change to a different unit for distance: the light second. That is per definition the distance a photon of light ray travels in one second:
For instance, it takes a photon about to travel from the sun to the Earth. Thus, the distance from the sun to the Earth is . That is equivalent to .
Ok, let’s be puzzled for a while: how can at the same time be both at the left side and at the right side of the Earth? That doesn’t make any sense!!!! What is wrong with this new theory? The answer is: nothing!
It is us, mixing stuff up. Who said that it is ‘at the same time’?!? Nobody (with perhaps for a moment us as the exception). and agree upon the event: a comet hits the moon. This physical phenomenon is not disputed at all. It happened. They don’t agree that it took place at the same time according to their clocks.
But this is not all: according to at the moment of the impact spaceship was at a distance of from the moon. But just calculated that she was from the moon. One cannot be at two different distance form the moon at the same time!
Ok, let’s push this somewhat further and see if we can get a contradiction.
We do know, from that the event took place at . Then, definitely has passed Earth. has reconstructed this event from observation Event got the information of event from and backed out the coordinates of the event in her coordinate system. From these data, can easily predict when she will see the impact. That is obviously later than the time of the event: the photons have to travel to her. How can we compute when literally sees the event?
That is remarkably easy: we know that according to the event tokes place at . At that moment and that place a photon was generated that moves in her direction. Since the velocity of each photon is always , we can easily find the time when sees the photon, i.e. detect it at location . The photon has to travel a distance at a speed of . That will take 1.33 s. The photon started traveling at time . Its trajectory according to is .
Thus, the photon gets measure at event : . Thus we have our third event:
And as we by now kind of expected: indeed, then is spaceship on the right side of the Earth. What does say about this event? He receives the coordinates of from and plugs them in, in the inverse LT:
Now does this make any sense? It does! If we concentrate on only and what he observes and knows:
- observes -comet hits moon:
- the comet actually hits the moon:
- observes that the comet hits the moon:
Obviously, if the actual impact is at positive , then will see it before does as for positive time is closer the moon than . And this is all reflected in the events. Moreover, if you would compute the events as will model things, you will find event just based on event and the motion of spaceship according to (and when it will encounter a photon that was generated at the actual impact of the comet on the moon). Do the calculation yourself and see, that nothing strange happens.
We can draw the position of Earth, moon and spaceship in space-time plot. It is customary to use as horizontal axis the or coordinate and as the vertical one or . will see the Earth and moon standing still and thus draw a vertical line in the space-time diagram for each of them: they do not change position, but their time is changing, i.e. the clock ticks. would draw for spaceship a straight line moving from left bottom to upper right as the spaceship moves in the positive direction.
Similarly, will draw a vertical line for spaceship itself, as in the frame of reference of the spaceship, obviously, does not move. The Earth and moon move to the left, thus their trajectories are straight line from the bottom right to the upper left in the -diagram.
At some moment in time-space the comet impacts the moon and a photon is moving in the negative -direction towards the Earth. Somewhat later, this photon is received by Earth. In the -diagram this is a straight line from lower right to upper left.
In the animation below the whole scenery is shown from the perspective of on the left side and from on the right side. The diagrams are made such, that the event “spaceship passes Earth” is simultaneous in both diagrams, i.e. it happens for both observers at their time equal to 0. All other events happen at different times according to the clocks of the observers.
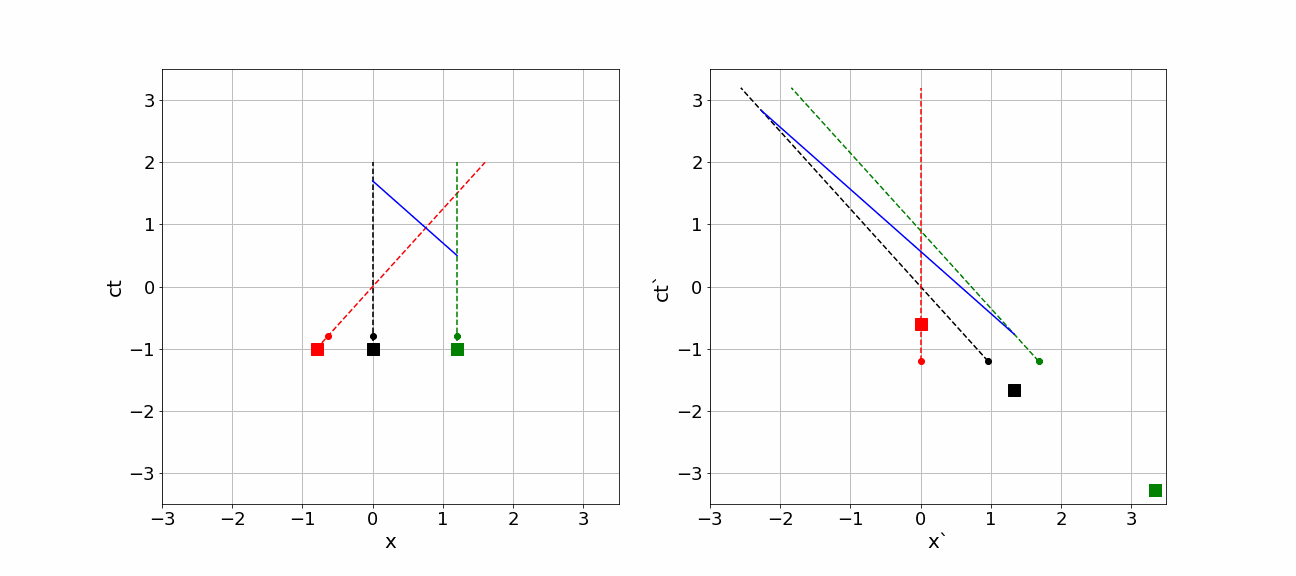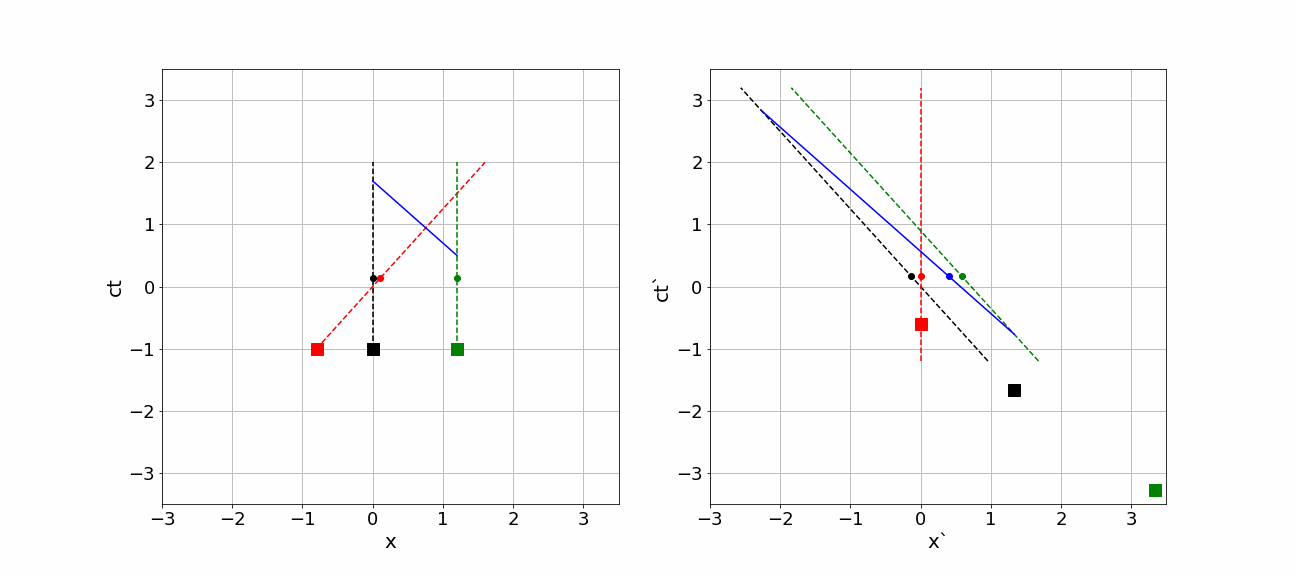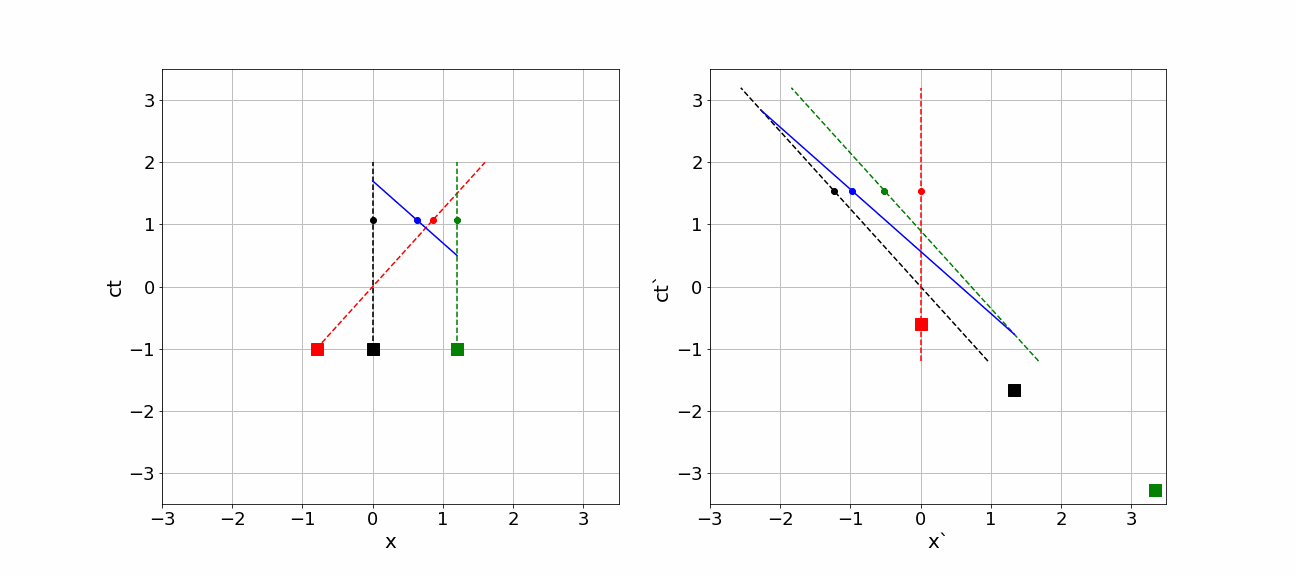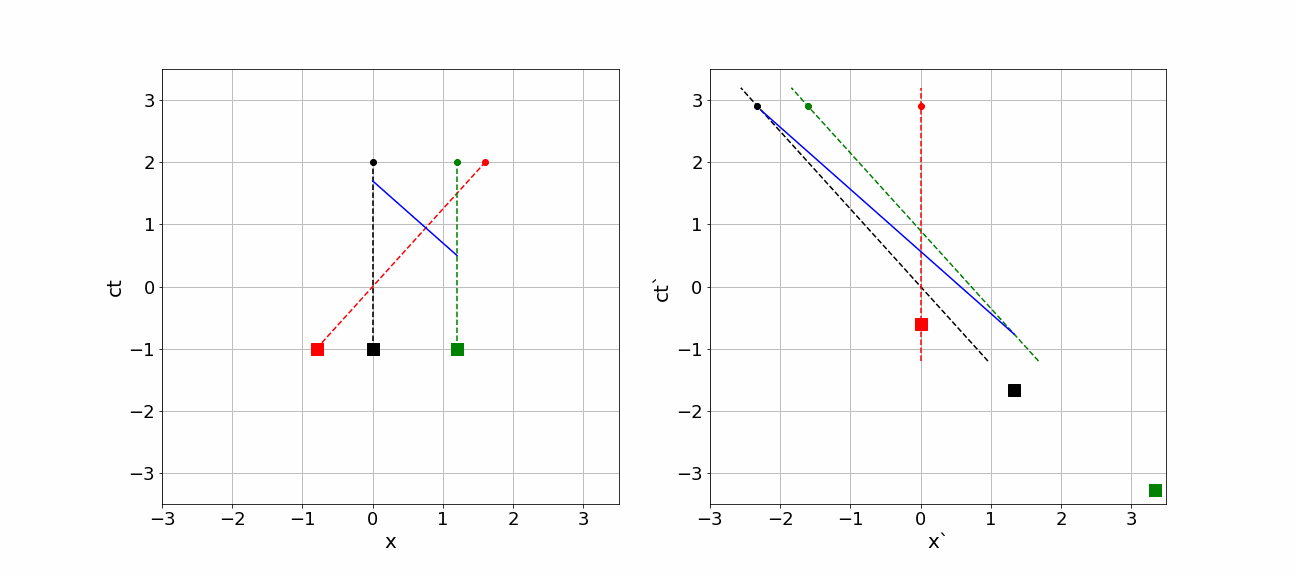
Figure 6:An animation of events as seen by different observers.
An animation is given above.
the three squares represent the position of Earth, moon and spaceship according to at ls. In the diagram for , these three are, of course, on a horizontal line as they are at the same time according to . However, sees that differently: there are absolutely not at the same time!!!
Earth, moon and spaceship do travel in the space-time diagrams. Their trajectories are shown by dashed lines. Their space-time location is represented by the (moving) dots. The diagrams are made such, that indeed both observers pass each other at and . The dots represent, where according to (left diagram) and (right diagram) Earth, moon and spaceship are at a certain time on the clock of that observer. Note that both position and time have really different values if you compare the diagrams of and .
In both diagrams, at some point in time the comet impacts the moon and a photon starts traveling in the negative and -direction. The photon is shown by the blue dot. Again nothing happens at the same time. But the order of events is the same: first the photon is emitted and only after that it is observed. That should of course hold!
Notice that the photon is emitted at ls according to and observed at . So for , the photon traveled for 1.2ls (and covered a distance of : of course, photons travel with velocity c). However, for this is quite different: the photon is emitted at , that is much earlier than reports. Moreover, it is only registered by on . It traveled for on the clock of !!
Puzzled by this all? Confused? Hard to believe?
Welcome the ‘Magical World of Relativity’. And don’t worry: you will get used to it. Moreover, we will develop a mathematical framework that helps us and prevents our failing intuition to take the wrong path.
Conclusions:
We need to be careful with interpreting distances and times, things are not what they seem at first glance.
Within the framework of one observer nothing funny happens.
We better work with well defined events: they represent physical phenomena happening. Both observers will agree upon these and on the logic, e.g. first the impact than the observation of a photon - not the other way around!
Time & Space¶
Here we have a look at the consequences of axioms 1 & 2. We know how two observers and (moving away with ) transform their respective coordinates into each other, via the Lorentz transformation.
We will look at the consequences for time and space coordinates.
Relativity of simultaneity
From the Lorentz transformation it is clear that time is not universal anymore ( in general). This is a large step from Newton and Galileo. Now the time coordinate is mixed somehow with the space coordinates depending on the speed .
Let us consider 2 events in the reference frame of ;
event A with coordinates
and event B with .
If the two events in are simultaneous, i.e. , then in they are in general not! Simultaneity is relative!
Even though the first term the second term is never zero unless , and in general.
In words: The events A and B that are simultaneous for , are never simultaneous for , unless the events are happening at the same place.
Relativität der Gleichzeitigkeit as Einstein called it, is the first very counterintuitive consequence by simple application of the Lorentz transformation. Our brains are not trained and build to cope with this aspect of nature. There is just no evolutionary advantage to it as all relevant speeds are much smaller than the speed of light.
Time dilation
We investigate how time intervals between a stationary and a moving observers are transformed. We can expect that these time intervals are not the same.
Figure 7:Clock stationary according to but moving for .
If you consider the sketch above, we see how time intervals are counted for a moving observer and for an observer in the rest frame. A light ray is traveling between 2 mirrors. This up and down traveling of the light is a counter for the time. If you have never thought how time is measured, think a bit how a clock actually does that. Today, the second is defined as a (very large) number of tiny energy transitions (vibrations) of the Caesium-133 atom (see e.g. Atomic Clock).
Consider the time light travels for the observer who sees the clock moving with velocity . The clock counts one unit of time, if the light has gone from the bottom mirror to the top one and back to the bottom mirror. Thus from bottom to top takes . This means that the length of the light path from bottom mirror to top mirror is equal to as light travels with velocity . In that same period of time, the top mirror has moved a distance , as the clock and thus the mirrors move with velocity with respect to observer . Now, we can relate the length of the light path from the bottom to the top mirror to the size of the clock, and the displacement of the mirror, : where we used Pythagoras, see Figure 8.
Figure 8:Light path in a moving clock.
We can solve this for the time that the stationary observer puts to the moving clock
We see directly that the time the stationary observer records is larger than the moving observer itself which is just (the time in his rest frame)! The time interval gets longer/dilated by the -factor.
with and the proper time or eigen time in the rest frame.
Note: a time interval is also the counting of your heart. That means the moving observer ages more slowly compared to the observer at rest. See the examples below for some experimental evidence of the time dilation.
Conclusion: moving clocks run slower, time gets stretched
Length contraction
The length of moving objects becomes smaller/contracted for the observer at rest. To explain this effect, we consider a moving rod with velocity and with length in the rest frame.
Now that we have seen that time intervals are no longer universal, we need to think about:
Normally, we measure the length of an object by seeing how many times a measuring stick fits in the object. We obviously do this in the frame of reference in which the object doesn’t move. There we don’t need to worry about the moment we start at the left side of the object and arrive with our measuring stick on the right side. But if we would do so in a frame of reference in which the object is moving, that wouldn’t work of course. By the time we would reach the right side of the object, it would no longer be at its starting position when we began our measurement and the number of times our ruler fits in the object is now influenced by the motion of the right side of the object.
To measure the length of a moving object, we thus need a different strategy. What we could do, is having a very long ruler fixed in our system. The object is moving past it. If we have two observers, one concentrating on the left side of the object and the other on the right side, we could ask them to measure the position of the left and right side of the object along the ruler at the same time. Then the difference of the left and right side on the ruler will give us the length of the object.
Thus: the length is measured from the difference of two events in space-time of the front and the back of the rod. We will call the events and . As we measure size, we require: , that is the measurements are done simultaneously in . According to , the length of the rod is , nothing special here.
Next, we transform the events and to :
For the difference between and is of course the length of the rod. It doesn’t matter for whether or not the coordinates the left and right side of the rod are measured at the same time. The rod is not moving in the frame of . Thus gets as length of the rod:
with the proper length of the rod, i.e. the length according to an observer moving with the rod.
Now we invoke the Lorentz transformation for the two events and to find the relation between the coordinates used by the two observers:
As we measure at the same time in , we have .
The length of the moving object observed by the stationary observer is not the same as the length in the rest frame. The length observed by the stationary observer gets smaller/contracted by compared to the length in the rest frame of : .
Conclusion: moving rods are shorter, space shrinks
Paradox: twins and barns¶
There are many variants of the following paradox. The word paradox already implies that there is only an apparent contradiction, not a real one. Here we will formulate the paradox with a ladder & barn and resolve it, but you can also think about it as a train & tunnel, or tank & trench etc. The resolution is always the same.
Let’s analyze the situation in detail using the Lorentz transformation. Later you can analyze it again qualitatively using a Minkowski-diagram which is quite insightful.
Our above “analysis” was a bit short: using length contraction. It is also a bit ‘dangerous’ as length contraction assumes simultaneous events in one frame.
We will consider how both observers would actually measure things in their respective frames of reference and in which order these happen. It turns out that both points of view are correct, but with a twist. We define 4 events to analyze the situation.
Event 1: right end ladder at left door barn
Event 2: right end ladder at right door barn
Event 3: left end ladder at left door barn
Event 4: left end ladder at right door barn (not really needed)
The four events are sketched in the figure below
Figure 10:Four events of the ladder & barn paradox
Note: the size of the ladder in the sketch above is of course open for debate between the two observers :-).
Observer Barn () will conclude that the ladder fits inside the barn and actually is inside the barn if Event 3 is earlier than Event 2, according to the clock of observer . If, however, Event 3 is later than Event 2, the ladder does not fit. Similarly, observer Ladder () will draw the same conclusions, but based on the clock of observer .
Let’s analyze these events. We will denote the coordinates of observer as and those of observer as . Both observers agree that they will call the position of the left door the origin, that is . Moreover, they agree that at the moment the right end of the ladder is at the left door, they will set their clocks to 0. Remember: according to observe , the length of the ladder is = 10 m, which happens to be the size of the barn according to . We anticipate that will conclude that the ladder fits.
Next, we need to give the events their space-time coordinates, e.g. in the frame of e and transform these coordinates according to the LT to the frame of . This is done below, where we used: = proper length of barn, i.e. in the rest frame of the barn and = proper length of ladder, that is in the rest frame of the ladder. Note:
| Event | Barn | Ladder |
|---|---|---|
| 1 | ||
| 2 | ||
| 3 |
As we see, according to , the left and right end of the ladder are exactly at the same moment at the left and right door of the barn, respectively (time coordinate of events 2 & 3 ). Consequently, observer measures that the ladder (just) fits into the barn as anticipated by us. So can close both doors and have the ladder inside the barn.
However, if we look at events 2 & 3 according to , we see that measures that the right end of the ladder is much earlier at the right door (event 2 ), than the left end is at the left door (event 3 ). So, according to , when the ladder hits the right end of the barn, the left part of the ladder is still left from the left door, thus outside the barn. The ladder does not fit. Of course, sees that closes the doors of the barn, but contrary to what says: 'I closed the doors simultaneously and the ladder was in my barn", will respond: “that may be true for you, but I clearly observed that you first shut the right door, while the left was still open. Then you quickly opened the right door to let the ladder pass and only after a while, when the left side of the ladder was just inside your bar, you closed the left door. The ladder was never inside the barn with both doors closed!”
The paradox is, that both observers are right. Again we see demonstrated that simultaneous for one does not necessarily mean simultaneous for another. Very counter intuitive and yet: very true.
As you see both observers do not agree where the ladder is when the left door is closed. Where for the barn observer both doors close at the same time, this does not happen for the ladder observer.