Skip to article frontmatterSkip to article content

4.5.1Exercises, examples & solutions

4.5.1.1Exercises

4.5.1.2Answers

Solution to Exercise 1

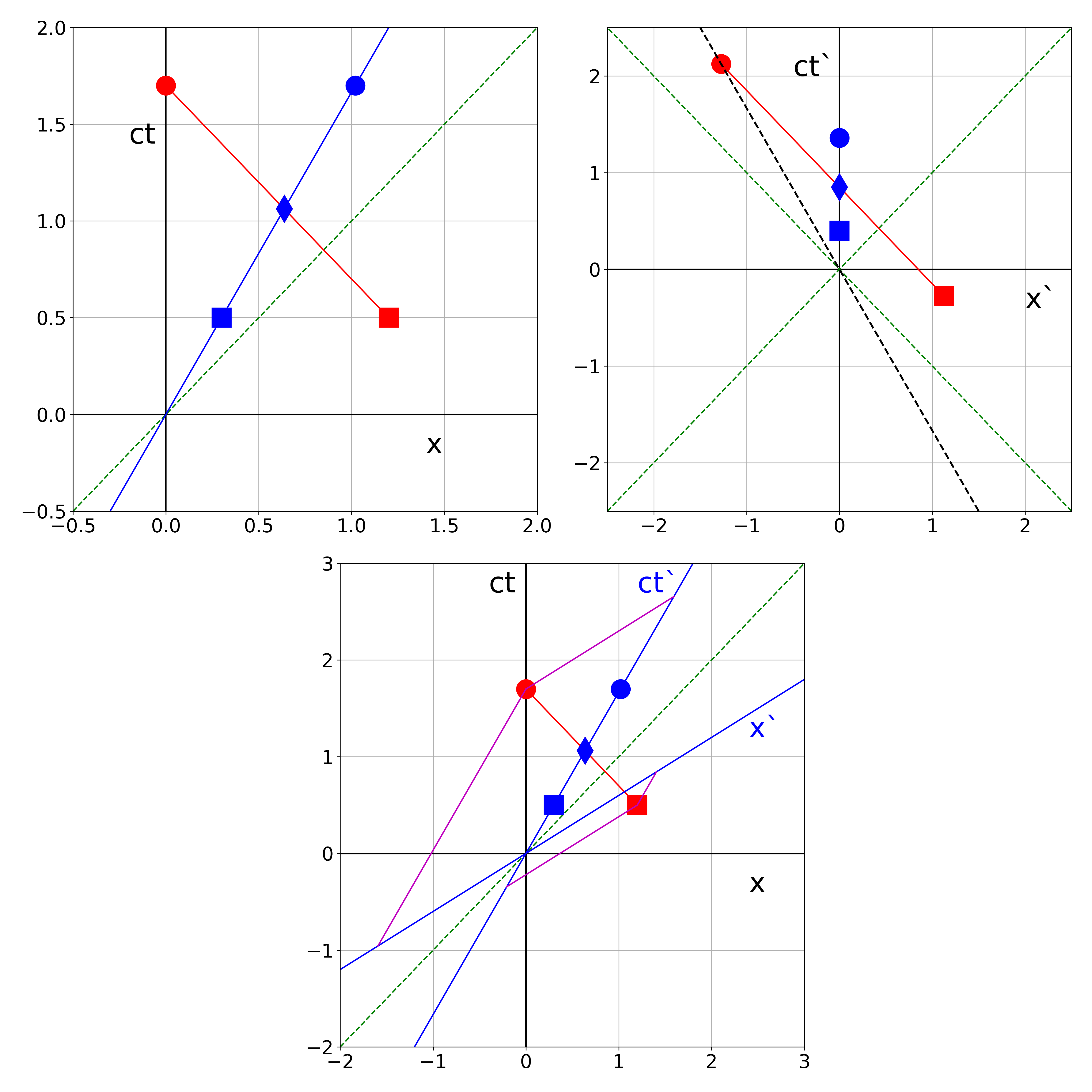
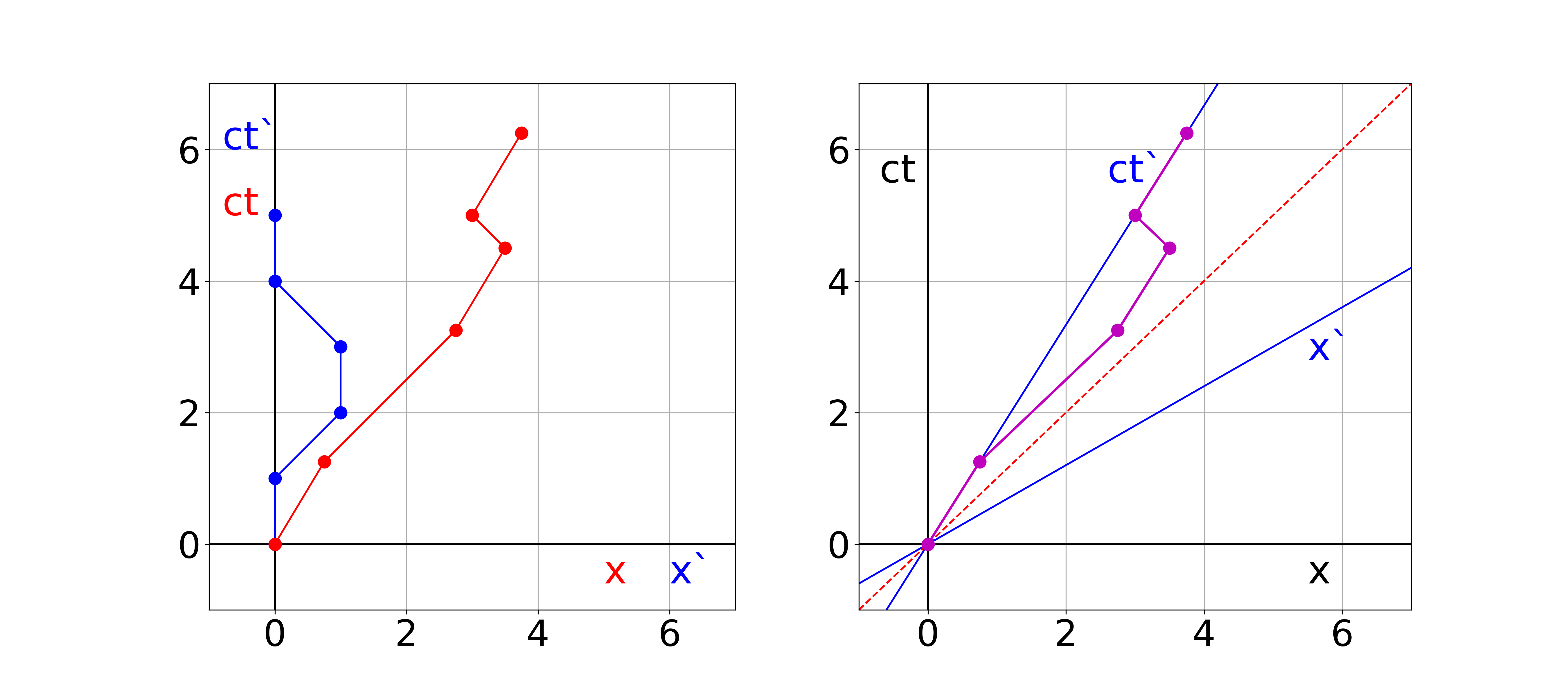
a. E1: (ct1,x1)=(1,0)(ct_1, x_1) = (1,0) and E2: (ct2,x2)=(0,1)(ct_2, x_2) = (0,1)

b. E3: (ct3,x3)=(1,3)(ct_3, x_3) = (1,3) and E4: (ct4,x4)=(−2,1)(ct_4, x_4) = (-2,1)

→Δs342=(1+2)2−(3−1)2=5 time like\rightarrow \Delta s_{34}^2 = (1+2)^2 - (3-1)^2 = 5 \text{ time like}
(2)

c. E5: (ct5,x5)=(1,2)(ct_5, x_5) = (1,2) and E6: (ct6,x6)=(3,4)(ct_6, x_6) = (3,4)

→Δs562=(1−3)2−(2−4)2=0 light like\rightarrow \Delta s_{56}^2 = (1-3)^2 - (2-4)^2 = 0 \text{ light like}
(3)

d. Transform to S′S': V/c=12/13→γ=13/5V/c = 12/13 \rightarrow \gamma = 13/5

ct′=γ(ct−Vcx)x=γ(x−Vcct)\begin{split} ct' &= \gamma \left ( ct - \frac{V}{c} x \right ) \\ x &= \gamma \left ( x - \frac{V}{c} ct \right ) \end{split}
(4)

E1: (ct1′,x1′)=(13/5,−12/5)(ct'_1, x'_1) = (13/5,-12/5) and E2: (ct2,x2)=(−12/5,13/5)(ct_2, x_2) = (-12/5,13/5)

→Δs12′2=(13/5+12/5)2−(−12/5−13/5)2=0 light like\rightarrow \Delta s^{'2}_{12} = (13/5+12/5)^2 - (-12/5-13/5)^2 = 0 \text{ light like}
(5)

E3: (ct3′,x3′)=(−23/5,27/5)(ct'_3, x'_3) = (-23/5,27/5) and E4: (ct4,x4)=(−38/5,37/5)(ct_4, x_4) = (-38/5,37/5)

→Δs34′2=(−23/5+38/5)2−(27/5−37/5)2=225/25−100/25=5 time like\begin{split} \rightarrow \Delta s^{'2}_{34} &= (-23/5+38/5)^2 - (27/5-37/5)^2 \\ &= 225/25 - 100/25 = 5 \text{ time like} \end{split}
(6)

E5: (ct5′,x5′)=(−11/5,14/5)(ct'_5, x'_5) = (-11/5,14/5) and E6: (ct6′,x6′)=(−9/5,16/5)(ct'_6, x'_6) = (-9/5,16/5)

→Δs56′2=(−11/5+9/5)2−(14/5−16/5)2=0 light like\rightarrow \Delta s^{'2}_{56} = (-11/5+9/5)^2 - (14/5-16/5)^2 = 0 \text{ light like}
(7)

Of course, for all cases we find Δs′2=Δs2\Delta s'^2 = \Delta s^2 : distance defined according to our Minkowski inproduct is a Lorentz invariant, i.e. the same for all inertial observers.

Solution to Exercise 2

For SS:

E1:(ct1,x1,y1,z1)=(0,4,0,0)E1: (ct_1, x_1, y_1, z_1) = (0,4,0,0)
(8)

E2:(ct2,x2,y2,z2)=(5,0,3,0)E2: (ct_2, x_2, y_2, z_2) = (5,0,3,0)
(9)

δs122=(0−5)2−(4−0)2−(0−3)2−(0−0)2=0\delta s^2_{12} = (0-5)^2 - (4-0)^2 - (0-3)^2 - (0-0)^2 = 0
(10)

light-like of course, as we deal with a light pulse.

For S′S': LT with V/c=4/5→γ=5/3V/c = 4/5 \rightarrow \gamma = 5/3

ct′=53(ct−45x)x′=53(x−45ct)y′=yz′=z\begin{split} ct' &= \frac{5}{3} \left ( ct - \frac{4}{5}x \right ) \\ x' &= \frac{5}{3} \left ( x - \frac{4}{5}ct \right ) \\ y' &= y \\ z' &= z \end{split}
(11)

Thus:

E1:(ct1′,x1′,y1′,z1′)=(−16/3,20/3,0,0)E1: (ct'_1, x'_1, y'_1, z'_1) = (-16/3,20/3,0,0)
(12)

E2:(ct2′,x2′,y2′,z2′)=(25/3,−20/3,3,0)E2: (ct'_2, x'_2, y'_2, z'_2) = (25/3,-20/3,3,0)
(13)

δs12′2=(−16/3−25/3)2−(20/3+20/3)2−(0−3)2−(0−0)2=4129−4029−819=0\begin{split} \delta s^{'2}_{12} &= (-16/3-25/3)^2 - (20/3+20/3)^2 - (0-3)^2 - (0-0)^2 \\ &= \frac{41^2}{9} - \frac{40^2}{9} - \frac{81}{9} =0 \end{split}
(14)
Solution to Exercise 3

We start with writing down the LT. As V/c=12/13V/c = 12/13 we have γ=13/5\gamma = 13/5. Thus, for this case LT reads as:

ct′=135(ct−1213x)x′=135(x−1213ct)\begin{split} ct' &= \frac{13}{5} \left ( ct - \frac{12}{13}x \right ) \\ x' &= \frac{13}{5} \left ( x - \frac{12}{13}ct \right ) \end{split}
(15)

a.

Δs2≡(ct2−ct1)2−(x2−x1)2=(4−3)2−(5−3)2=−3\begin{split} \Delta s^2 &\equiv (ct_2 - ct_1 )^2 - (x_2 - x_1 )^2 \\ &=(4-3)^2-(5-3)^2 \\ &= -3 \end{split}
(16)

b. event E1:

ct1′=135(3−12133)=35x1′=135(3−12133)=35\begin{split} ct'_1 &= \frac{13}{5} \left ( 3 - \frac{12}{13}3 \right ) = \frac{3}{5} \\ x'_1 &= \frac{13}{5} \left ( 3 - \frac{12}{13}3 \right ) = \frac{3}{5} \end{split}
(17)

event E2:

ct2′=135(4−12135)=−85x2′=135(5−12134)=175\begin{split} ct'_2 &= \frac{13}{5} \left ( 4 - \frac{12}{13}5 \right ) = -\frac{8}{5} \\ x'_2 &= \frac{13}{5} \left ( 5 - \frac{12}{13}4 \right ) = \frac{17}{5} \end{split}
(18)

c.

Δs′2≡(ct2′−ct1′)2−(x2′−x1′)2=(−85−35)2−(175−35)2=12125−19625=−3\begin{split} \Delta s'^2 &\equiv (ct'_2 - ct'_1 )^2 - (x'_2 - x'_1 )^2 \\ &=(-\frac{8}{5}-\frac{3}{5})^2-(\frac{17}{5}-\frac{3}{5})^2 \\ &= \frac{121}{25} -\frac{196}{25} = -3 \end{split}
(19)
Solution to Exercise 4

Lorentz Transformation

ct=γ(ct′+Vcx′)x=γ(x′+Vcct′)with Vc=35 and γ=54\begin{split} ct &= \gamma \left ( ct' + \frac{V}{c} x'\right ) \\ x &= \gamma \left ( x' + \frac{V}{c} ct'\right )\\ \text{with } &\frac{V}{c} = \frac{3}{5} \text{ and } \gamma = \frac{5}{4} \end{split}
(20)

This gives:

E0: (ct0,x0)=(0,0)(ct_0, x_0)=(0,0)
E1: (ct1,x1)=(5/4,3/4)(ct_1, x_1)=(5/4,3/4)
E2: (ct2,x2)=(13/4,11/4)(ct_2, x_2)=(13/4,11/4)
E3: (ct3,x3)=(9/2,7/2)(ct_3, x_3)=(9/2,7/2)
E4: (ct4,x4)=(5,3)(ct_4, x_4)=(5,3)
E5: (ct5,x5)=(25/4,15/4)(ct_5, x_5)=(25/4,15/4)

This gives the two required plots.

left: S and S' in the same diagram; right: Minkowski diagram.

Figure 1:left: SS and S′S' in the same diagram; right: Minkowski diagram.

Solution to Exercise 5
top left: S , top right: S', bottom: Minkowski diagram.red: square - comet hits moon, diamond - photon registered by Space Ship, circle - photon detected by earthblue: corresponding position of S' according to S and its Lorentz transform for S'Minkowski diagram: pink lines show the intersection with the ct' and x' axes, i.e. the coordinates according to S'

Figure 2:top left: SS , top right: S′S', bottom: Minkowski diagram.
red: square - comet hits moon, diamond - photon registered by Space Ship, circle - photon detected by earth
blue: corresponding position of S′S' according to SS and its Lorentz transform for S′S'
Minkowski diagram: pink lines show the intersection with the ct′ct' and x′x' axes, i.e. the coordinates according to S′S'

Classical Mechanics & Special Relativity for Starters
Spacetime and 4-vectors
Classical Mechanics & Special Relativity for Starters
4-Momentum & E=mc²