5.5.1Worked Example¶
In class you have seen the Superballs example. Let’s dive more deep into what is happening.
Watch the superballs again.
Consider Figure 2, if you let a smaller and a larger ball drop together, stacked on top of each other, the smaller ball will bounce back much stronger (higher) than if you let the small ball fall without stacking it on the lager ball. How can that happen?
Figure 2:Bouncing balls.
To explain this we use the Galilean Transformation (GT). Consider the following situation depicted in Figure 2.
- 1 Both balls are falling with velocity towards the ground.
- 2a The larger ball just hit the ground. As the mass of the ground is much larger than that of the large ball, it is (elastically) reflected, i.e. the direction of the velocity is reversed but the magnitude stays the same. The small ball is still moving downwards with .
- 2b We apply a GT of the observer (yellow star) from the ground to an observer moving with the larger ball. The observer moving with the larger ball sees the smaller ball moving with towards it.
- 3a The smaller ball hits the larger ball and is reflected due to its smaller mass. In the frame of the observer on the larger ball, the smaller ball now moves with away from it.
- 3b We apply a GT of the observer (yellow star) from the larger ball back to an observer on the ground. For the observer on the ground the larger ball has velocity upwards from 2a, therefore the smaller ball has velocity upwards.
The smaller ball has now velocity instead of if you drop it without the larger ball. NB: If you would use three balls instead of two, the third ball would have a velocity of using the same reasoning as above.
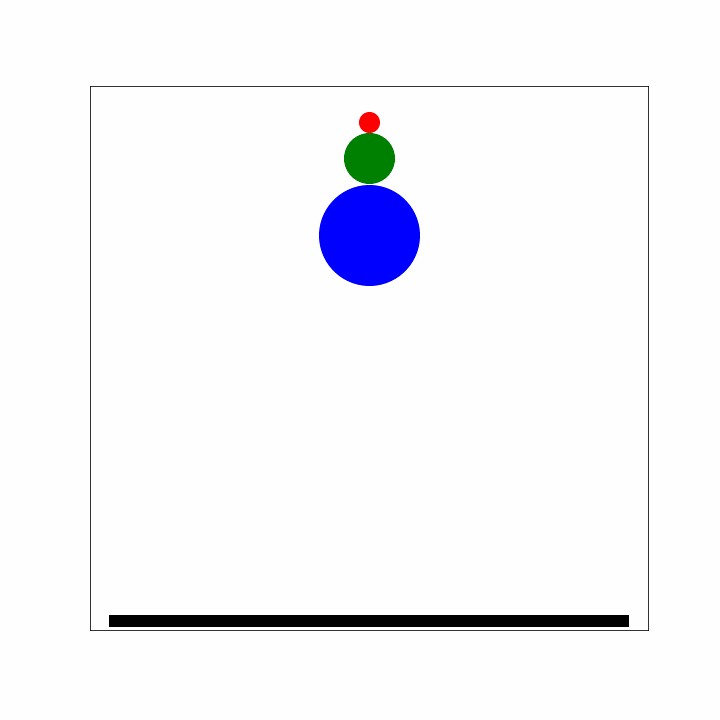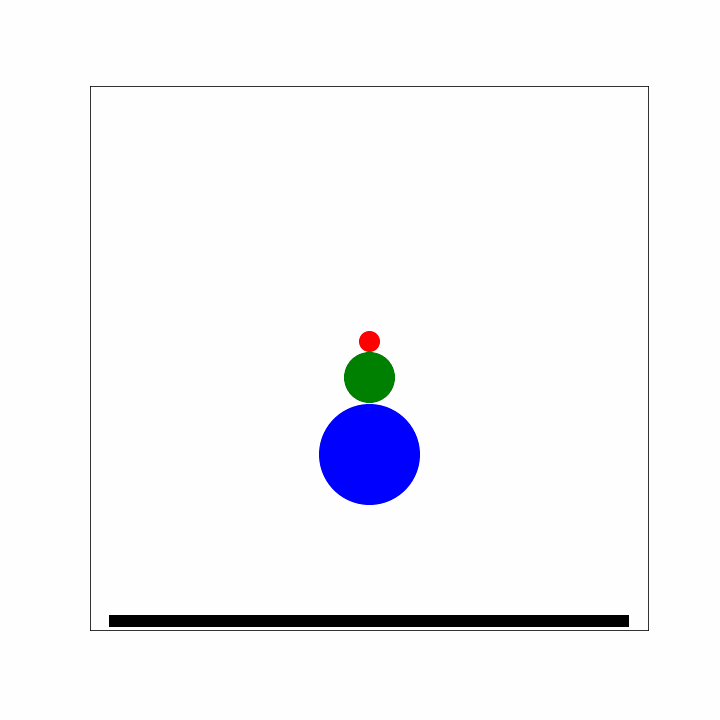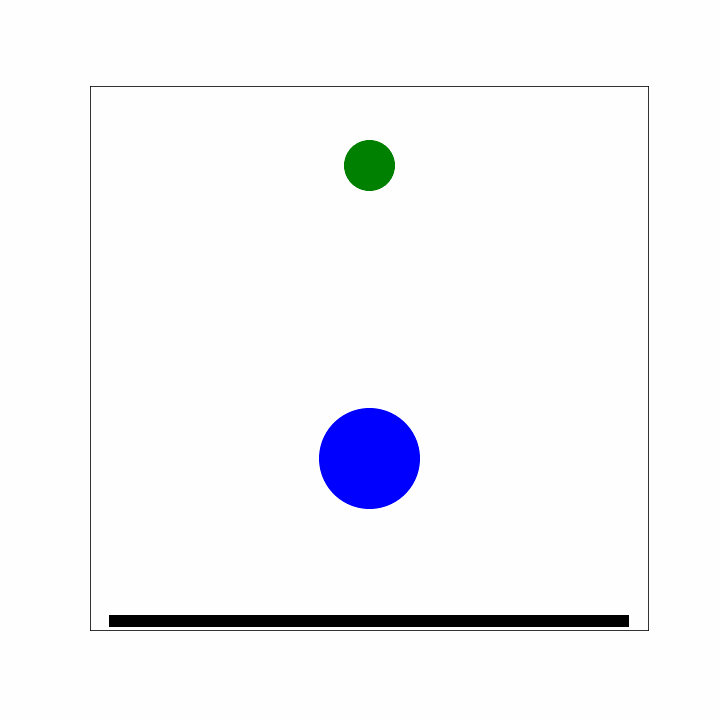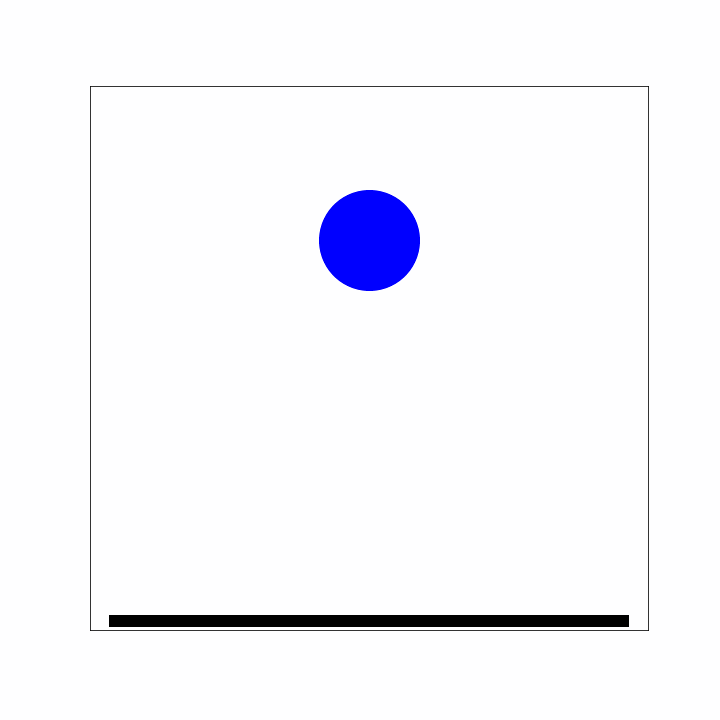
Figure 3:Bouncing of three (super)balls.
How much higher does the smaller ball fly with velocity compared to ?
Answer
We equate the kinetic energy when the ball is just reflected with the potential energy when the ball reached it maximal height before falling back.
Therefore the ball with flies 9 times higher.
What is very fishy about this whole outcome?
In situation 1) the kinetic energy is , but in situation 3b) it is while the potential energy is zero in both cases. This clearly does not add up! But energy must be conserved under all circumstances!
The conclusion is, that we did make an approximation and did not solve the energy and momentum conservation equations for elastic collisions. Even for the case there is some momentum transfer. If you solve for the velocity of after the collision with , you obtain
For you indeed see . Thus the smaller ball will have a smaller velocity than reasoned above and the larger ball with also have a smaller velocity (in the experiment you can clearly notice that it does not fly as high as when it drops without the small ball on top). In real life, the balls also deform which makes the collision inelastic.
In a later chapter we will deal with collisions and pay attention to this limit in much more detail.
5.5.2Examples¶
5.5.3Demo¶
A ball is bouncing at a wall. The mass of the wall is much greater than that of the ball. So, acceleration of the wall or changes in momentum of the wall can be ignored.
On the left side, we see this from the perspective of an observer, S, standing next to the wall. The right side shows what observer S’, who is traveling with the ball as it moves towards the wall, sees. Notice, that both S and S’ are inertial observers. That is, they keep their velocity and are no part of the collision. What would Galilei say?
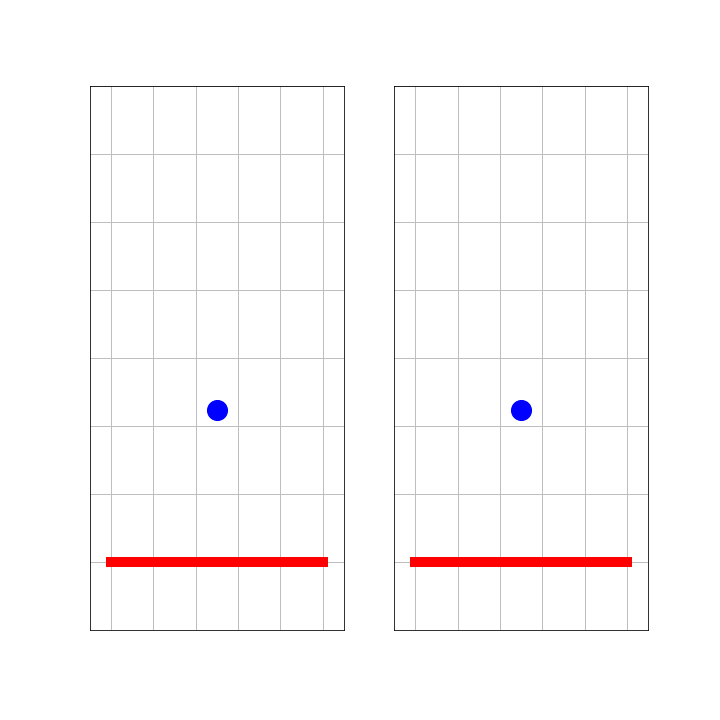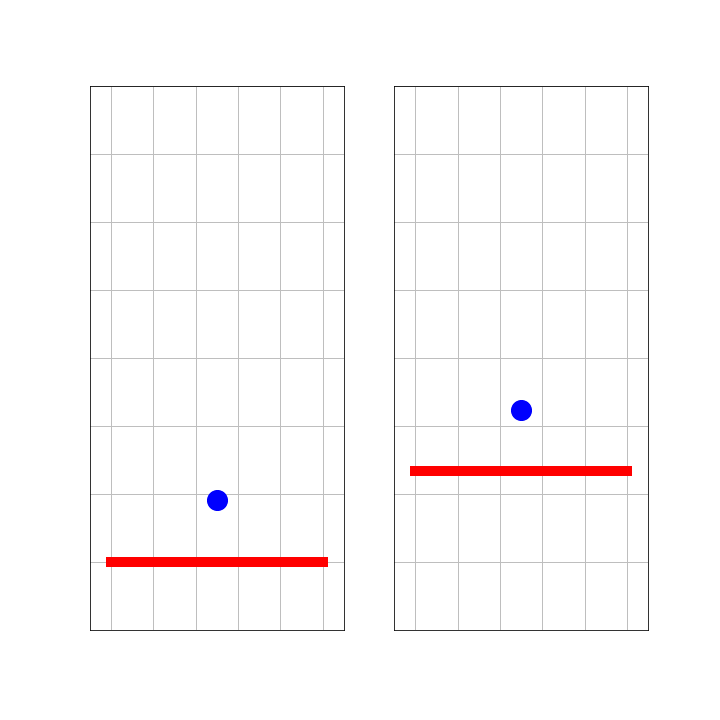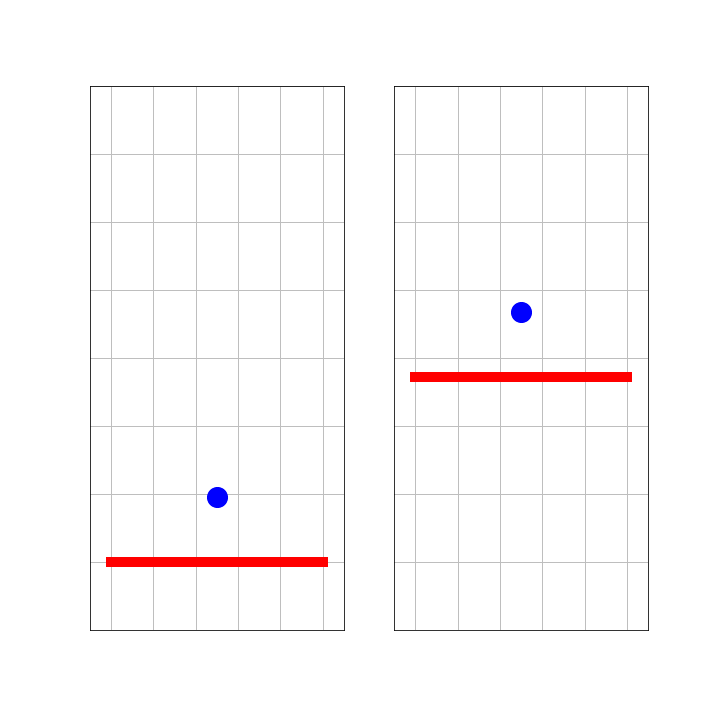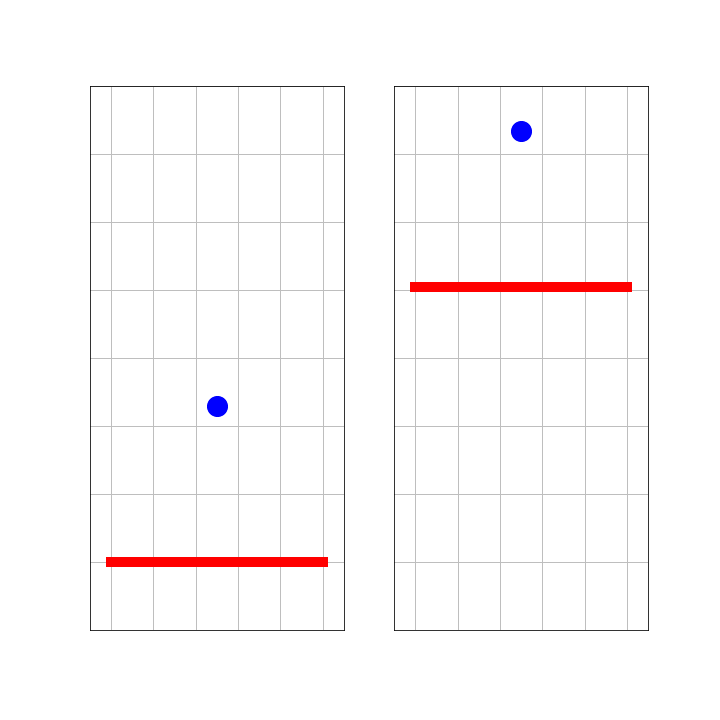
Figure 6:Ball bouncing at a wall.
5.5.4Exercises¶
5.5.5Answers¶
Solution to Exercise 1
First we make a new sketch, now showing the two observers and and their axis. We have made the velocity of the object red, the color of . And we have given the coordinates of the front and back of the train in grey as these are specified according to . We do this, as it is is crucial to realize that we have ‘mixed’ information.
The velocity of the object is according to . The observer in the train, , sees a different velocity.
The observer in the train will denote the position of the front of the train by and of the back . Both are, according to , fixed values. But will see that differently.
According to , the object moves with velocity . Note that this is a negative value, otherwise the object will not hit the back of the train.
will describe the trajectory of the object by: with . Thus, the object will hit the back of the train at:
What does observe? It will write for the trajectory of the object (where we used that the object was released in the middle of the train at and both observers chose that as their origin).
According to also the back of the train is moving. It follows a trajectory , since at the back of the train was at position according to . The two will collide when
Hence we have and as times of collision. But we already found . If we substitute this in we get
Thus, indeed both observers see the collision at the same moment.
Sneak Preview: much to our surprise, when we enter the world of Special Relativity, this will no longer be the case!
Solution to Exercise 2
The particle will ‘collide’ with the bump. This might cause the particle to start moving to the left. How to analyse this situation?
Perhaps it is easier when we view this from the point of view of an observer moving with the table.
Now we have a situation of a particle moving over a friction less table with velocity . If we use conservation of energy, we can write down:
where we have taken as the height above the table and denote the velocity of at some point by . The initial height is zero and the initial velocity is .
So, if the initial velocity is such that , the particle will go over the bump and come back to height . It will thus pass the bump and then continue moving with velocity . For the original observer this means: the bump will pass the particle and after passing the particle is again laying still (but not at the same position!).
If, on the other hand is such that , the particle will not reach the top of the bump: it has insufficient kinetic energy. In stead it will stop at some height and then fall of the bump again. It will continue with velocity at the flat part of the table. To the original observer this means that first climbs the bump and returns to get a velocity on the flat part of the table.
The final possibility is . In that case the particle will exactly reach the top of the bump and stop there.
N.B. We have assumed that the bump is not too steep, because in such a case the particle will have a real collision with the bump. Think, for instance, of the bump as a sudden step. Then no matter how fast the particle is moving, it will not end up on the step, but bounce back.
Solution to Exercise 3
First, a sketch:
It is a 1-dimensional problem, so an -axis will do. We denote the velocity of your opponent (as seen by you) by and of the snowball . The inertial system of you is and you are sitting in the origin . Similarly, you opponents inertial system is with origin and finally the snowball has inertial system and the snowball sits in the origin .
Your perspective
require:
Your opponent’s perspective
require: since is in . Thus
Same time of course. Position: your opponent concludes she is not moving and this she is hit at .
- The snowballs perspective.
According to the snowball . Thus, require:
And, again the snowball will conclude that it all happened in its origin.
Galilei Transformation
We now have three different time/place coordinates for the event ‘snowball hits opponent’.
We could have found this directly from a GT.
a) from to : we need to take into account that at the origins do not coincide. Instead is shifted over a distance L w.r.t.
Thus: and we get indeed
b) We do a similar exercise for to :
Thus: and we get